Welcome back to the Deep Learning Interview Prep Series! 🚀
So far, we’ve covered the fundamentals of neural networks, backpropagation & gradient descent, training challenges & best practices, loss functions, optimization algorithms, and regularization techniques.
Now, we shift gears to architectures. First up: Convolutional Neural Networks (CNNs) the backbone of modern computer vision.
1. Conceptual Understanding
A Convolutional Neural Network (CNN) is a neural network specialized for grid-like data structures, such as images (2D grid of pixels) or audio spectrograms (2D time-frequency grids).
Unlike fully connected layers, CNNs exploit spatial locality and weight sharing through convolutional filters, making them both efficient and powerful.
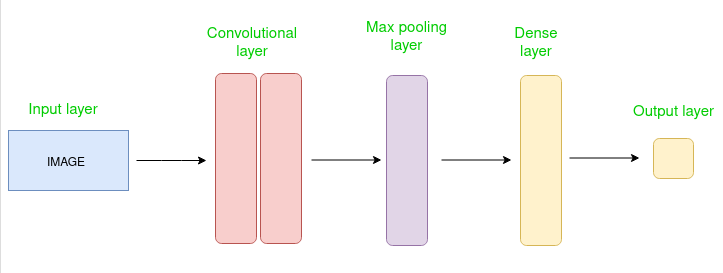
Key Components of a CNN
1. Convolutional Layer
Uses learnable filters (kernels) that slide across the input.
Each filter extracts a particular pattern (e.g., edge, texture, shape).
Mathematical Operation (2D convolution):
Where:
I= input image
K = filter/kernel
(i, j) = pixel position
Example: A 3×3 edge-detection filter will highlight edges in an image.
2. Activation Function (ReLU)
Adds non-linearity:
Prevents CNNs from collapsing into linear models.
Enables learning of complex, hierarchical features.
3. Pooling Layer
Reduces spatial dimensions (downsampling), retaining important information.
Max Pooling:
Average Pooling: Takes average of values.
Pooling provides translation invariance (object moves slightly → prediction remains stable).
4. Fully Connected Layer (FC)
After convolution + pooling, the feature maps are flattened and passed through FC layers to make predictions.
5. Softmax (for classification)
Final layer converts logits into probabilities:
Why CNNs Work Better Than Fully Connected Networks
Aspect Fully Connected Network CNN Parameters Huge (each pixel connected to each neuron) Small (filters are shared) Locality Ignores spatial structure Exploits local patterns Translation Invariance Weak Strong (via pooling & shared weights) Scalability Poor for high-dimensional data Excellent
CNNs scale efficiently to large images while learning hierarchical features (edges → textures → object parts → objects).
2. Applied Perspective
CNNs dominate computer vision applications, but also extend beyond images.
Common Applications
Image Classification: Cats vs dogs, handwritten digit recognition.
Object Detection: YOLO, Faster R-CNN (detect & localize objects).
Semantic Segmentation: Pixel-level classification (e.g., U-Net in medical imaging).
Face Recognition: Embedding-based similarity.
Self-driving Cars: Lane detection, obstacle recognition.
NLP & Speech: Character-level text models, speech spectrogram analysis.
Example: Image Classification Pipeline
Input: 224×224 RGB image.
Convolution + ReLU (extract features like edges).
Convolution + ReLU (extract higher-level patterns).
Pooling (reduce size, keep important info).
Fully Connected (combine features).
Softmax (output class probabilities).
3. System Design Perspective
CNNs in production face unique engineering challenges.
Key Considerations
Model Size & Efficiency
Early CNNs (VGG-16) → 138M parameters (too heavy).
Modern alternatives: ResNet (skip connections), EfficientNet (scaling), MobileNet (lightweight).
Deployment Environment
Cloud/Server: Use ResNet/EfficientNet for high accuracy.
Edge Devices (mobile, IoT, drones): Use MobileNet, SqueezeNet, or quantized models.
Optimization Techniques
Quantization (float32 → int8).
Pruning (remove redundant filters).
Knowledge Distillation (large → small model transfer).
Monitoring in Production
Watch for data drift (lighting, camera quality).
Use periodic retraining pipelines.
4. Interview Questions
Q1. What problem do CNNs solve compared to fully connected networks?
Q2. Explain convolution and pooling with intuition.
Q3. What is the effect of padding and stride in convolution?
Q4. Why do deeper CNNs perform better? What are the drawbacks?
Q5. Compare VGG, ResNet, and MobileNet.
5. Solutions
Q1. What problem do CNNs solve compared to fully connected networks?
Fully connected networks explode in parameters with high-dimensional inputs (e.g., 224×224×3 ≈ 150k features).
CNNs reduce parameters by weight sharing and local receptive fields, making them scalable.
Q2. Explain convolution and pooling with intuition.
Convolution: Extracts local features (edges, shapes).
Pooling: Reduces resolution, provides invariance to small shifts.
Q3. What is the effect of padding and stride in convolution?
Padding: Preserves input size, avoids shrinking after convolution.
Stride: Controls step size. Larger stride → smaller feature maps.
Q4. Why do deeper CNNs perform better? What are the drawbacks?
Deeper CNNs learn hierarchical features (edges → textures → parts → objects).
Drawbacks: prone to vanishing gradients, require large datasets, heavy compute.
Q5. Compare VGG, ResNet, and MobileNet.
VGG: Known for its simple yet deep architecture, VGG set a strong benchmark for CNNs. However, its large size and slow inference make it impractical for modern, resource-constrained scenarios.
ResNet: Introduced skip connections, which effectively solved the vanishing gradient problem and allowed training of very deep networks. The trade-off is that ResNets can be computationally heavy, limiting their deployment on edge devices.
MobileNet: Built for efficiency, MobileNet is lightweight and fast, making it ideal for mobile and embedded applications. Its main drawback is slightly lower accuracy compared to ResNet and EfficientNet.
Conclusion
CNNs were a breakthrough in deep learning, powering nearly every modern computer vision system from self-driving cars to facial recognition.
They reduce parameter explosion, leverage local patterns, and achieve translation invariance. But deploying them efficiently requires careful architecture choice (ResNet vs MobileNet vs EfficientNet).
Next in the Series:
CNNs revolutionized deep learning by making image-based tasks feasible and efficient. They remain a backbone for many real-world applications in vision, healthcare, and autonomous systems.
In our next article, we’ll move to Recurrent Neural Networks (RNNs) exploring how neural nets handle sequential data like text, speech, and time series.