🔹 First Post in the Deep learning Series
Welcome back to our Machine Learning / Deep Learning interview prep series! After exploring the foundational ML algorithms like logistic regression, decision trees, and clustering methods, we now begin our journey into Deep Learning—starting with the most fundamental concept: Neural Networks.
This post dives deep into:
Conceptual understanding of neural networks
Practical applications and training insights
System design perspective
Tricky interview questions
Fully detailed answers
📘 1. Conceptual Understanding
What is a Neural Network?
A neural network is a function approximation technique inspired by the structure of the human brain. It consists of layers of interconnected units called neurons, where each neuron receives inputs, applies a weight and bias, and outputs a transformed result via an activation function.
The simplest neural unit is the perceptron. It computes a weighted sum of inputs and applies a step activation function to make a binary decision.
Here:
w0 is the bias term
w1,...,wm are weights
f is the activation function
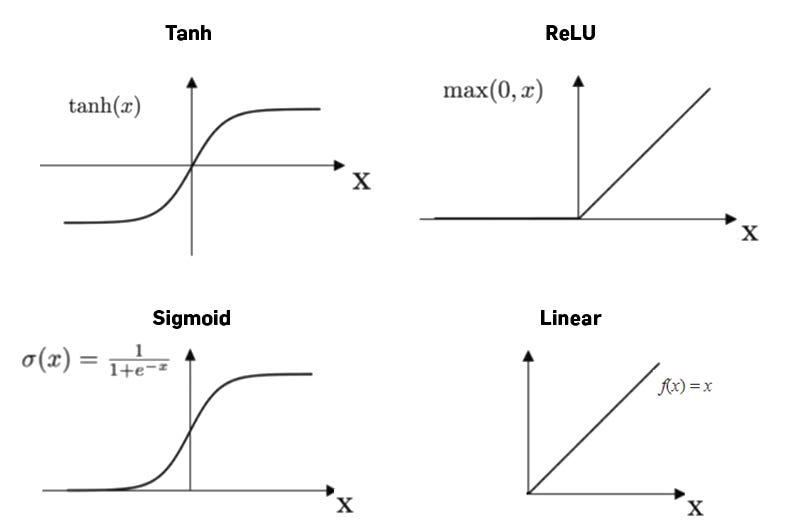
Activation Functions
Without activation functions, stacking layers would just result in another linear model. Non-linearity enables the network to capture complex relationships.
Common activation functions include:
Sigmoid: Squashes output to (0,1), useful for binary classification.
\(sigma(z) = \frac{1}{1 + e^{-z}}\)Tanh: Zero-centered, output between (-1,1).
\(\tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}\)ReLU (Rectified Linear Unit): Simple and fast, outputs zero for negatives and identity for positives.
\(\text{ReLU}(z) = \max(0, z)\)
Multi-Layer Perceptrons (MLPs)
An MLP consists of:
An input layer
One or more hidden layers
An output layer
Each layer's output is passed as input to the next. MLPs are feedforward networks, meaning data flows in one direction—no cycles or feedback.
🧪 2. Applied Perspective
Training a Neural Network
Training is done using forward propagation followed by backward propagation:
Forward Propagation: Compute predictions layer by layer.
Loss Calculation: Compare predictions to true outputs using a loss function like Mean Squared Error or Cross Entropy.
Backward Propagation: Apply the chain rule to compute gradients of loss w.r.t each weight.
Gradient Descent: Update weights to reduce loss:
\(w_i := w_i - \alpha \cdot \frac{\partial L}{\partial w_i}\)where α is the learning rate, and L is the loss.
Where Neural Networks Excel
Neural networks are preferred when:
Relationships between features are non-linear
The feature space is large or unstructured
Automatic feature learning is needed (e.g. image, audio, text data)
They power applications like:
Image recognition
Text classification
Language translation
Recommendation engines
🛠️ 3. System Design Perspective
Engineering Considerations
Overfitting: Common due to high capacity. Use regularization, dropout, and early stopping.
Training Time: Deep networks can take long to converge. Use GPUs and optimized libraries.
Hyperparameter Tuning: Includes learning rate, number of layers, batch size, etc. Use grid or random search.
Data Preprocessing: Normalize inputs for better convergence.
Interpretability
Neural networks are often considered black boxes. Interpretation tools like LIME and SHAP help understand feature contributions.
4. Interview Questions
What is a Perceptron and how does it work?
Why are activation functions necessary in neural networks?
Compare Sigmoid, Tanh, and ReLU activation functions.
Explain forward and backward propagation.
What is the vanishing gradient problem and how can it be mitigated?
🧠 5. Solutions
Q1: What is a Perceptron and how does it work?
A perceptron is the simplest form of a neural network. It computes a weighted sum of the inputs, adds a bias term, and applies an activation function to produce an output. If the weighted sum exceeds a threshold, the output is one class; otherwise, it's another. It's suitable only for linearly separable data.
Q2: Why are activation functions necessary in neural networks?
Activation functions introduce non-linearity, enabling the network to approximate complex patterns. Without them, a neural network—no matter how many layers—would behave like a linear model and fail to learn intricate relationships in data.
Q3: Compare Sigmoid, Tanh, and ReLU activation functions.
Sigmoid: Outputs values between 0 and 1. Good for probabilities but suffers from vanishing gradients and is not zero-centered.
Tanh: Outputs between -1 and 1. Zero-centered and better than sigmoid, but still suffers from vanishing gradients.
ReLU: Outputs zero for negative inputs and identity for positives. It’s efficient, sparsely activates neurons, and avoids vanishing gradient in most cases.
Q4: Explain forward and backward propagation.
Forward propagation computes output predictions by passing inputs through the layers.
The loss function measures the difference between predictions and true values.
Backward propagation computes how each weight contributes to the error using derivatives and the chain rule.
Weights are updated using gradient descent, minimizing the error.
Q5: What is the vanishing gradient problem and how can it be mitigated?
When training deep networks with sigmoid or tanh activations, gradients can become very small as they propagate backwards, causing early layers to learn very slowly. This is called the vanishing gradient problem.
It can be addressed using:
ReLU activation (avoids saturation)
Batch normalization
Residual connections (e.g., in ResNets)
📚 References & Further Reading
🔜 What’s Next?
In our next article, we'll go deeper into how neural networks are trained—including detailed walkthroughs of backpropagation, gradient flow, and optimization algorithms.
This foundation will prepare us to tackle CNNs, RNNs, and attention-based architectures down the line.